 Сегодня на занятии произойдет чудо. Репетитор по математике и физике за все время существования сайта впервые с вами заговорит! Так уж получилось, что новая тенденция по созданию репетиторами записей своих занятий не обошла стороной и меня. Этой мой первый видеоурок, я пока даже не до конца уверен в правильности написания этого выражения (кстати, если эти строки читает эксперт, напишите, пожалуйста, в комментариях какое написание является грамматически правильным, заранее большое спасибо). Поэтому я решил выбрать для начала несложную задачу, в которой требуется найти уравнение прямой в форме с угловым коэффициентом по графику соответствующей линейной функции.
Сегодня на занятии произойдет чудо. Репетитор по математике и физике за все время существования сайта впервые с вами заговорит! Так уж получилось, что новая тенденция по созданию репетиторами записей своих занятий не обошла стороной и меня. Этой мой первый видеоурок, я пока даже не до конца уверен в правильности написания этого выражения (кстати, если эти строки читает эксперт, напишите, пожалуйста, в комментариях какое написание является грамматически правильным, заранее большое спасибо). Поэтому я решил выбрать для начала несложную задачу, в которой требуется найти уравнение прямой в форме с угловым коэффициентом по графику соответствующей линейной функции.
Сразу хочу сказать, что точки A и B принадлежат графику, хотя по используемому изображению может показаться, что они «выколоты». Это, конечно, неверное с методической точки зрения обозначение, но автор задания почему-то выбрал именно его. Если бы эти точки действительно были «выколоты», то их абсциссы следовало бы исключить из области определения соответствующей линейной функции, но тогда с чисто геометрической точки зрения данная фигура уже не являлась бы прямой.
В данном задании требуется написать уравнение прямой, изображенной на рисунке, в форме с угловым коэффициентом. Здесь на рисунке я намеренно закрасил обе точки, чтобы не возникало никаких двояких толкований. Точки A и B принадлежат графику данной линейной функции.
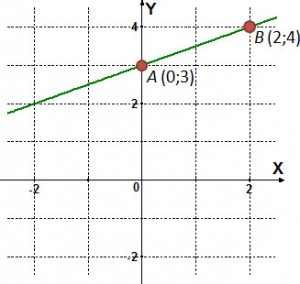
График линейной функции, по которому требуется составить уравнение прямой в форме с угловым коэффициентом
Напомню, что общее уравнение прямой на плоскости в форме с угловым коэффициентом имеет вид:
![]()
где ![]() — угловой коэффициент,
— угловой коэффициент, ![]() — параметр, ответственный за смещение прямой вдоль оси
— параметр, ответственный за смещение прямой вдоль оси ![]()
Итак, задача сводится к отысканию значений параметров ![]() и
и ![]() Из рисунка видно, что прямой принадлежат точки
Из рисунка видно, что прямой принадлежат точки ![]() и
и ![]() Это означает, что при подстановке координат этих точек в общее уравнение прямой с угловым коэффициентом, будут получаться верные равенства. То есть мы получим две верных уравнения:
Это означает, что при подстановке координат этих точек в общее уравнение прямой с угловым коэффициентом, будут получаться верные равенства. То есть мы получим две верных уравнения:
![]()
С учетом того, что параметры ![]() и
и ![]() и в том, и в другом уравнении одинаковы, данные уравнения можно объединить в систему:
и в том, и в другом уравнении одинаковы, данные уравнения можно объединить в систему:
![Rendered by QuickLaTeX.com \[ \begin{cases}3 = k\cdot 0+b, \\ 4=k\cdot 2+b.\end{cases} \]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-1659502c9b1ba08db5b2fd95e677bf54_l3.png)
Из первого уравнения автоматически получаем, что параметр ![]() Подставляя это значение во второе уравнение, получаем
Подставляя это значение во второе уравнение, получаем ![]() или
или ![]() откуда
откуда ![]() Итак, уравнение данной прямой в форме с угловым коэффициентом имеет вид:
Итак, уравнение данной прямой в форме с угловым коэффициентом имеет вид:
![]()
Частный преподаватель математики в районе «Тёплый Стан»
Сергей Валерьевич