
Прямая Эйлера — это такая прямая, на которой лежат следующие точки:
Нарисуем треугольник общего вида. Единственное, пусть он будет остроугольным. Хотя на самом деле все дальнейшие рассуждения с небольшими косметическими поправками будут справедливы и для тупоугольного треугольника. Проведём в этом треугольнике все высоты. Как известно, в треугольнике либо сами высоты, либо их продолжения пересекаются в одной точке. Назовём её точкой G. По-другому эта точка называется «ортоцентром»:
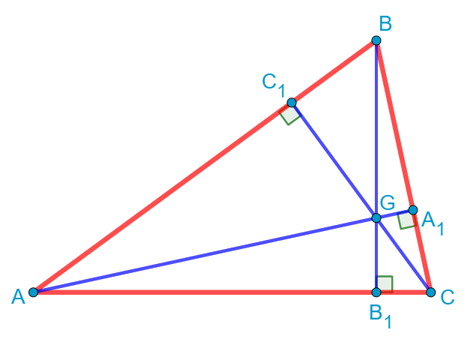
Соединим теперь основания высот A1 и C1 отрезком. И докажем, что треугольник C1BA1 подобен треугольнику ABC. Ну, действительно. У них есть общий угол B. Кроме того, если рассмотреть прямоугольный треугольник CC1B, то косинус угла B в нём равен отношению прилежащего катета BC1 к гипотенузе BC: ![]() . С другой стороны, из прямоугольного треугольника ABA1 мы получаем, что косинус того же самого угла B равен отношению прилежащего катета BA1 к гипотенузе BA:
. С другой стороны, из прямоугольного треугольника ABA1 мы получаем, что косинус того же самого угла B равен отношению прилежащего катета BA1 к гипотенузе BA: ![]() :
:
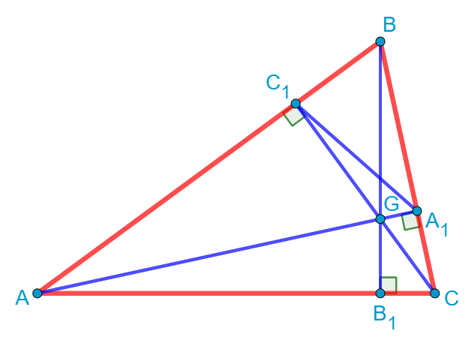
Ну и теперь мы видим, что общий угол B образован в наших треугольниках пропорциональными сторонами: ![]() . Значит, треугольники C1BA1 и ABC подобны. Причём их коэффициент подобия равен
. Значит, треугольники C1BA1 и ABC подобны. Причём их коэффициент подобия равен ![]() .
.
Обратим теперь внимание на то, что ![]() . Это означает, что сумма противоположных углов четырёхугольника GC1BA1 равна 180 градусам. Значит, вокруг него можно описать окружность:
. Это означает, что сумма противоположных углов четырёхугольника GC1BA1 равна 180 градусам. Значит, вокруг него можно описать окружность:
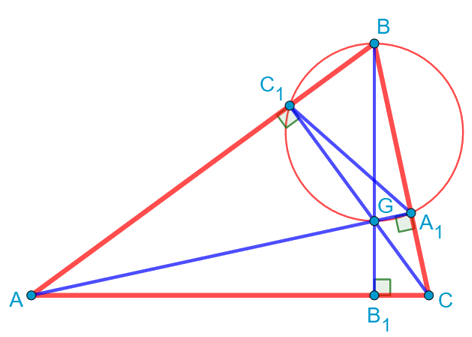
При этом отрезок BG будет являться диаметром этой окружности, поскольку на него опирается вписанный угол BA1G, который равен 90 градусов.
Проведём теперь серединные перпендикуляры к сторонам AB и AC. Они пересекутся в точке O, которая, как хорошо известно, является центром описанной около треугольника ABC окружности. То есть треугольник AOC будет равнобедренным, причём его боковые стороны по длине будут равны радиусу описанной окружности:
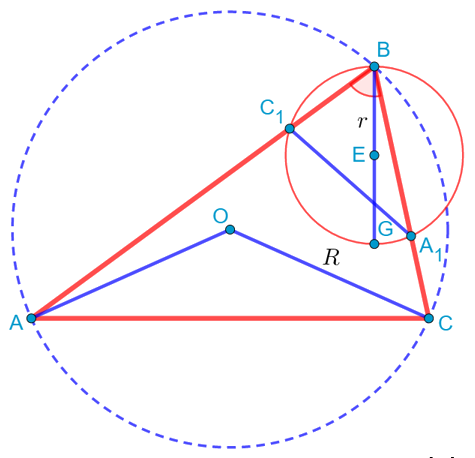
То есть мы получили, что вокруг подобных треугольников BC1A1 и ABC описаны окружности. Но коэффициент их подобия равен косинусу угла B. Но в подобных треугольниках одинаковым образом относятся все элементы, в том числе и радиусы описанных окружностей, поэтому ![]() .
.
Проведём теперь высоту OD в треугольнике AOC. Обратим внимание, что угол B является вписанным и опирается на дугу AC. Но на эту же дугу опирается и центральный угол AOC, который поэтому должен быть вдвое больше угла B. Но высота OD делит этот угол ровно пополам, так как она является одновременно и биссектрисой, проведённой к основанию равнобедренного треугольника. Значит, ∠B = ∠DOC:
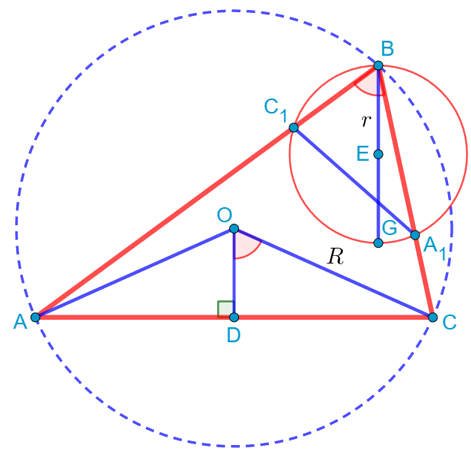
Но тогда косинус угла B мы можем расписать, используя треугольник DOC. В нём этот косинус равен отношению прилежащего катета OD к гипотенузе OC, которая равна радиусу описанной окружности R. И этот же косинус, как мы выяснили, равен отношению r к R: ![]() . Из последнего равенства получаем, что
. Из последнего равенства получаем, что ![]() или иначе
или иначе ![]() .
.
Проведём теперь отрезок BD, который будет являться медианой. Проведём также прямую через точки O и G. То есть через эти две точки проходит прямая, что, конечно, не удивительно, ведь мы знаем, что через две точки можно провести прямую, притом только одну. Эта прямая пересекает медиану BD в некоторой точке M:
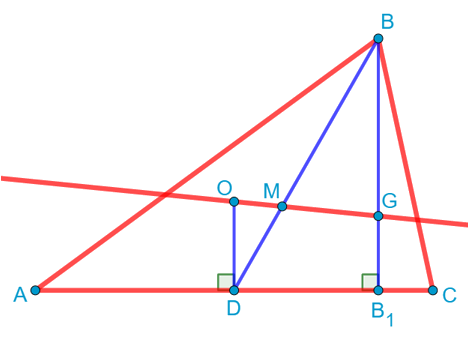
Как вы думаете, что это за точка? Уже догадались? А может быть уже знали и раньше? Если нет, то настало время удивляться! Посмотрите на треугольник OMD. Он подобен треугольнику MGB по двум углам: вертикальным и накрест лежащим при параллельных прямых. И мы даже знаем коэффициент подобия этих треугольников. Он равен 1:2. А значит, все стороны этих треугольников относятся как 1:2, в том числе и стороны DM и MB.
И что же у нас получилось? А получилось то, что точка M делит медиану BD в отношении 2:1, считая от вершины. А значит, точка M – это точка пересечения медиан треугольника или, как её по-другому называют, цетроид треугольника.
Таким образом мы доказали, что ортоцентр треугольника, центр описанной около него окружности и центроид этого треугольника лежат на одной прямой. Эта прямая и называется прямой Эйлера!
Факт существования прямой Эйлера насколько удивителен, что даже не всегда укладывается в голове. Специально для вас я подготовил поясняющую анимацию. Посмотрите её в видео на моём Youtube-канале.
Вне зависимости от типа треугольника, как угодно можно над ним издеваться, но эти три точки всегда будут лежать на одной прямой. Возможны, правда, случаи, когда эти точки совпадают. Например, для правильного треугольника все они сливаются в одну точку. Но если мы имеем дело не с этим тривиальным случаем, то все эти точки лежат на одной прямой. Прямой Эйлера.
И у этой прямой очень много других интересных свойств. Пишите в комментариях, стоит ли написать на эту тему отдельную статью. Успехов!
Материал подготовил репетитор по математике и физике Сергей Валерьевич
Спасибо за побадривающее доказательство и анимацию.Сергей Валерьевич,только этого материала достаточно,чтобы сделать вывод о Вашей высокой репетиторской квалификации!