В данной статье репетитором по математике и физике дается информация о том, как найти величину вписанного угла. Рассматривается определение вписанного угла, а также теорема о вписанном угле и следствия из этой теоремы. После этого дается подробный анализ решения задачи со вписанным углом.
| Вписанным углом называют угол, вершина которого принадлежит окружности, а стороны пересекают эту окружность. |
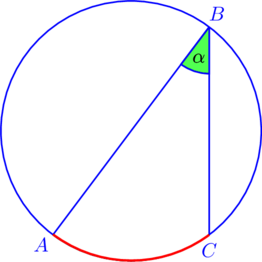
Например, на рисунке ![]() — вписанный, при этом он опирается на дугу
— вписанный, при этом он опирается на дугу ![]() .
.
| Величина вписанного угла в два раза меньше градусной меры дуги, на которую он опирается. |
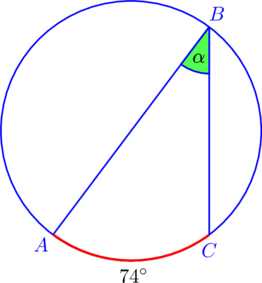
Например, на рисунке градусная мера дуги ![]() равна
равна ![]() . На эту дугу опирается вписанный
. На эту дугу опирается вписанный ![]() . Следовательно,
. Следовательно, ![]() .
.
К это теореме есть два важным следствия и одно замечание:
|
|
Вписанные углы, которые опираются на равные дуги (или на одну и ту же дугу), равны. Например, на рисунке: |
|
|
Вписанный угол, который опирается на полуокружность (иначе говоря, на диаметр окружности), равен |
|
|
Величина вписанного угла равна половине величины центрального угла, который опирается на ту же дугу. Например, на рисунке |
| Окружность с центром в точке |
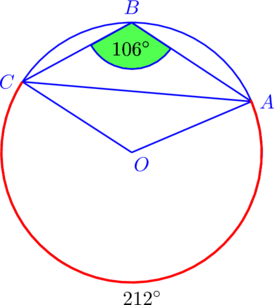
1. Заместим, что ![]() — вписанный. Следовательно, градусная мера дуги
— вписанный. Следовательно, градусная мера дуги ![]() , на которую он опирается, вдвое больше его градусной меры, то есть равна
, на которую он опирается, вдвое больше его градусной меры, то есть равна ![]() .
.
2. Тогда градусная мера дуги, на которую опирается центральный угол ![]() (это тоже дуга
(это тоже дуга ![]() , только «маленькая»), равна
, только «маленькая»), равна ![]() , так как градусная мера полной окружности равна
, так как градусная мера полной окружности равна ![]() .
.
3. Величина центрального угла, как известно, равна градусной мере дуги, на которую этот угол опирается. Следовательно, ![]() .
.
Репетитор математики на Юго-Западной
Сергей Валерьевич