Изучению методов решения задач по теме «Потенциал электростатического поля» следует уделять особое внимание. От того, насколько хорошо ученик усвоит данный материал, зависит глубина понимания последующих разделов курса физики (в первую очередь тем, связанных с постоянным и переменных электрическим током). Умение решать задачи на нахождение потенциала является, кроме того, одним из требований к Единому Государственному Экзамену (ЕГЭ) по физике 2012 года.

Прежде чем приступить к решению типовых задач, вспомним основные теоретическое сведения, связанные с этой темой:

• Электростатическое поле является потенциальным. Это означает, что работа сил электрического поля при перемещении заряда по любой замкнутой траектории равна нулю. Если же траектория перемещения заряда не является замкнутой,

Работа электрических сил при малом перемещении заряда

то работа электростатического поля в этом случае определяется следующим образом: ΔA = EqΔlcos α, где E — напряженность поля в данной точке, q — величина заряда, Δl — величина малого перемещения заряда, α — угол между направлением напряженности поля и перемещением заряда.

• Если переместить заряд q из точки с потенциальной энергией W₁ в точку с потенциальной энергией W₂, то разница этих энергий будет равна работе, которую совершит при этой электрическое поле: A = W₂ − W_1.

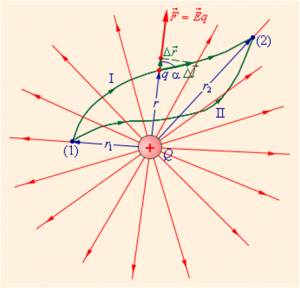
Работа, совершаемая полем при перемещении заряда из одной точки в другую, равняется разности потенциальных энергий заряда в этих точках

• Потенциал электрического поля — физическая скалярная величина, равная отношению потенциальной энергии электрического заряда в данной точке электростатического поля к величине этого заряда:

Потенциал — энергетическая характеристика поля. В международной системе единиц (СИ) единицей потенциала является вольт (В).

• Потенциал поля точечного разряда и заряженной сферы определяется соотношением:

где r — расстояние от заряда или центра сферы до данной точки пространства (в случае со сферой эта точка должна располагаться вне сферы), q — величина заряда, k = 9 · 10⁹ Н·м²/Кл² — постоянный коэффициент. Потенциал внутри сферы в любой точке одинаков и равен потенциалу на ее поверхности:

где R — радиус сферы.

• Работа по перемещению электрического заряда q из одной точки пространства в другую равна произведению этого заряда на разность потенциалов между этими точками: A₁₂ = q(φ₂ − φ₁).
• Напряжение между двумя точками однородного электростатического поля и напряженность этого поля связаны соотношением: U = Ed, где d — расстояние между эквипотенциальными поверхностями, которым принадлежат эти точки.

Приступим теперь к решению задач. Как и всегда рекомендую читателю решить их сперва самостоятельно, а полученные решения сравнивать с приведенными в статье. Некоторые задачи взяты из реальных вариантов ЕГЭ по физике разных лет, а также из пособий, рекомендованных для подготовки к этому экзамену.

Задача 1. При перемещении заряда между точками с разностью потенциалов 1 кВ электрическое поле совершило работу 40 мкДж. Чему равен заряд?

Решение: решаем устно. Из формулы A₁₂ = q(φ₂ − φ₁) получаем, что q = A / (φ₂ − φ₁) = 40 · 10 ^{− 6} / 10³ = 4 · 10 ^{− 8} Кл.

Ответ: 4 · 10 ^{− 8} Кл.

Задача 2. В однородном электрическом поле напряженностью 60 кВ/м переместили заряд 5 нКл. Перемещение, равное по модулю 20 см, образует угол 60⁰ с направлением силовой линии. Найти работу поля, изменение потенциальной энергии взаимодействия заряда и поля и напряжение между начальной и конечной точками перемещения. Дать ответы на те же вопросы для случая перемещения отрицательного заряда.

Решение: работу поля по перемещению заряда можно вычислить по формуле A = Eqlcos α = 60 · 10³ · 5 · 10 ^{− 9} · 0.2 · cos 60⁰ = 3 · 10 ^{− 5} Дж. Изменение потенциальной энергии в данном случае равно совершенной работе, следовательно: ΔW = —A = —3 · 10 ^{− 5} Дж (потенциальная энергия уменьшилась). Напряжение определяется через напряженность поля по формуле: U = Ed = Elcos α, поскольку в данном случае в заряд перемещали под углом к направлению силовых линий. Итак, U = 60 · 10³ · 0.2 · cos 60⁰ = 6000 В. В случае с отрицательным зарядом значения A и ΔW просто изменят знак.

Ответ: 3 · 10 ^{− 5} Дж, —3 · 10 ^{− 5} Дж, 6000 В, -3 · 10 ^{− 5} Дж, 3 · 10 ^{− 5} Дж, 6000 В.

Задача 3. Электрон переместился в ускоряющем электрическом поле из точки с потенциалом 200 В в точку с потенциалом 300 В. Найти кинетическую энергию электрона, изменение его потенциальной энергии и приобретенную скорость. Начальную скорость электрона считать равной нулю.

Решение: работу, которую совершило поле при перемещении электрона, находим следующим образом: A₁₂ = q(φ₂ − φ₁) = 1.6 · 10^-19 · (300 — 200) = 1.6 · 10^-17 Дж. Значит изменение потенциальной энергии электрона в поле равно: ΔW = —A = —1.6 · 10 ^{− 17} Дж. Это уменьшение компенсируется увеличением его кинетической энергии на такое же значение, что следует из закона сохранения энергии: E = 1.6 · 10 ^{− 17} Дж. Поскольку E = mυ² / 2, то υ = √(2E / m) = √(2 · 1.6 · 10 ^{− 17}/9.1 · 10 ^{− 31}) = 6 Мм/с.

Ответ: 1.6 · 10 ^{− 5} Дж, —1.6 · 10 ^{− 5} Дж, 6 Мм/с.

Задача 4. Какую разность потенциалов должен пройти электрон, чтобы его скорость увеличилась от 10 до 30 Мм/с?

Решение: изменение кинетической энергии электрона при прохождении такой разности потенциалов можно найти из соотношения: ΔE = mυ₂² / 2 — mυ₁² / 2 = 8 / 18  · 9.1 · 10 ^{− 31} · (30 · 10 ⁶)² = 3.6 · 10 ^{− 16} Дж. Это же изменение по закону сохранения энергии равняется работе, которую совершило при этом электрическое поле: E = —A = -3.6 · 10 ^{− 16} Дж. Используя соотношение, записанное в самом начале, получаем: φ₂ − φ₁ = A / q = -3.6 · 10 ^{− 16}/ 1.6 · 10^-19 = -2250 В.

Ответ: -2250 В.

Профессиональный репетитор
по физике и математике
Сергей Валерьевич