Медиана, высота и биссектриса треугольника

Автор

Среда, 12 сентября, 2012

Решение задач на нахождение длин высот, медиан и биссектрис треугольника по его сторонам

Для решения задач по геометрии, связанных с треугольниками, важно усвоить одну простую, но важную истину. Существует третий признак равенства треугольников («по трем сторонам»), из которого следует, что не существует двух различных треугольников с одинаковыми сторонами. Следовательно, зная длины всех сторон треугольника, можно узнать об этом треугольнике все, что нужно. В том числе длины его медиан, биссектрис и высот. Разберем более подробно, каким образом это можно сделать.

Теорема о длине высоты треугольника

Для нахождения длины высоты треугольника можно расписать его площадь двумя способами. Во-первых, используя формулу Герона, во-вторых, как половину произведения высоты на основание, к которому проведена данная высота.

    \[ S = p\sqrt{(p-a)(p-b)(p-c)} = \frac{1}{2}ah_a. \]

здесь p=\frac{a+b+c}{2} — полупериметр треугольника.

Из сравнения данных формул находим:

    \[ h_a = \frac{2\sqrt{p(p-a)(p-b)(p-c)}}{a}. \]

Отметим, что это лишь один из способов нахождения длины высоты треугольника по его сторонам, который удобен далеко не всегда. Существует огромное множество альтернативных способов, с которыми читатель может ознакомиться в предыдущих уроках.

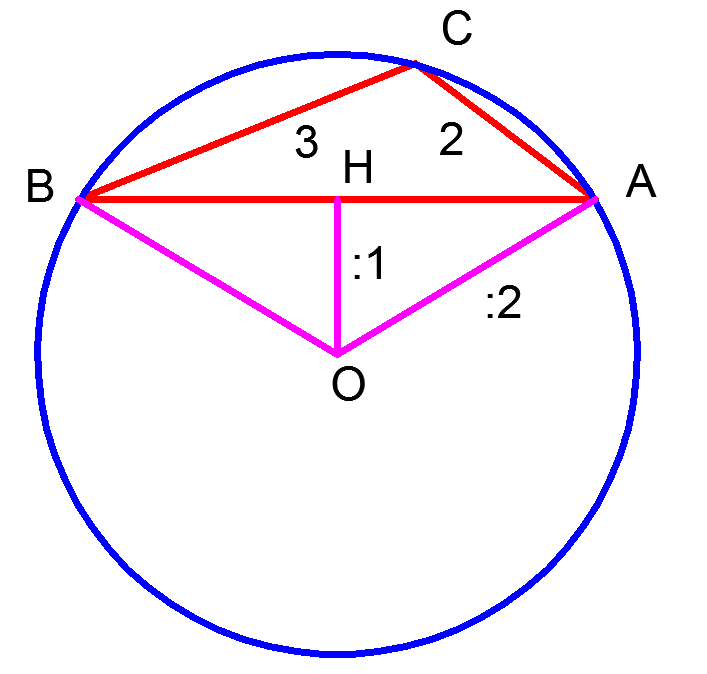
Пример 1. Известно, что расстояние от центра описанной окружности до стороны AB треугольника ABC равняется половине радиуса этой окружности. Найдите высоту треугольника ABC, опущенную на сторону AB, если она (высота) меньше \sqrt{\frac{3}{2}}, а две другие стороны равны 2 и 3.

Задача по геометрии на нахождение высоты треугольника

Решение. Треугольник BOA на рисунке является равнобедренным, поэтому ∠ OAH = ∠ OBH = 30° (катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы). Тогда ∠ BOA и соответствующая дуга окружности, на которую он опирается, равны по 120°. Тогда дуга, на которую опирается ∠ BCA, равна 240°, а значит сам угол ∠ BCA = 120°.

Площадь треугольника ABC находим по формуле: S =\frac{1}{2}\cdot BC\cdot AC\cdot\cdot\sin 120^0 = \frac{3\sqrt{3}}{2}. Длину стороны AB находим по теореме косинусов для треугольника ABC, она равна \sqrt{19}. С другой стороны, площадь треугольника есть половина произведения высоты на основание, к которому данная высота проведена. Отсюда выражаем требуемую длину высоты h=\frac{3\sqrt{3}}{\sqrt{19}}, что меньше \frac{\sqrt{3}}{2}. Случай с остроугольным треугольником ABC не подходит. Проверьте самостоятельно.

Задача для самостоятельного решения №1. В остроугольном треугольнике ABC BC = a, AC = b, ∠ ACB равен α. Найти высоту CD и ∠ ABC.

Показать ответ
Ответ:

    \[ \frac{ab\sin\alpha}{\sqrt{a^2+b^2-2ab\cos\alpha}} \]

    \[ \operatorname{arcsin}\frac{b\sin\alpha}{\sqrt{a^2+b^2-2ab\cos\alpha}} \]

Теорема о длине медианы треугольника

Медиана треугольника определяется через три его стороны по формуле:

    \[ m_a^2 = \frac{b^2+c^2}{2}-\frac{a^2}{4}, \]

где a, b, c — стороны треугольника, ma — медиана, проведенная к a. С доказательством этого утверждения интересующийся читатель может ознакомиться в видеоуроке.

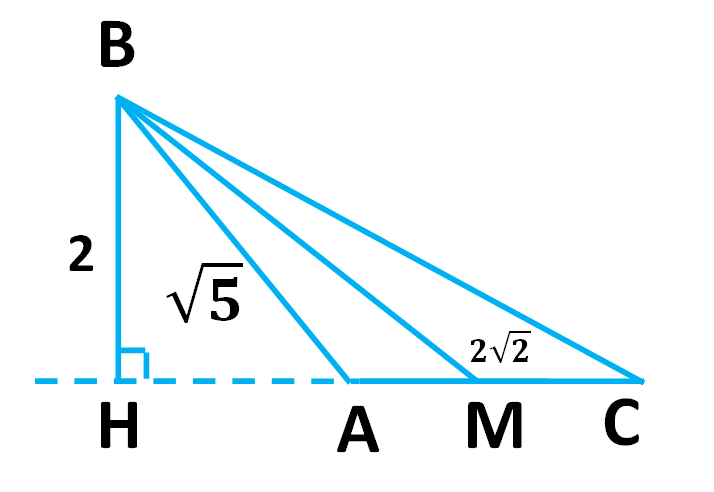
Пример 2. В треугольнике ABC со стороной AB = \sqrt{5} из вершины B к стороне AC проведены медиана BM = 2\sqrt{2} и высота BH = 2. Найдите сторону BC, если известно, что ∠ B + ∠ C < 90°.

Нахождение медианы треугольника по длинам его сторон

Решение. Из анализа условия задачи делаем вывод, что ∠ A — тупой. Действительно, ведь сумма всех углов в треугольнике равна 180°. Находим по теореме Пифагора длину HA = 1. Далее по теореме Пифагора находим длину HM = 2. Следовательно, AM = HM — HA = 1. При этом AM = MC = 1 (т. к. BM — медиана). Итак, HC = HA + AM + MC = 3. Следовательно, по теореме Пифагора BC = \sqrt{13}. Прямой подстановкой убеждаемся в справедливости ранее полученной формулы для длины медианы треугольника.

Задача для самостоятельного решения №2. В треугольнике ABC медианы, проведенные к сторонам AC и BC, пересекаются под прямым углом. Известно, что AC = b, BC = a. Найдите длину стороны AB.

Показать ответ
Ответ: \sqrt{\frac{a^2+b^2}{5}}.

Теорема о длине биссектрисы треугольника

Длина биссектрисы треугольника определяется по следующей формуле: l_a^2=bc-a_ba_c, где l_a — биссектриса, проведенная к стороне a; a_b, a_c — отрезки, на которые биссектриса делит сторону a, прилежащую к сторонам b и c соответственно. С доказательством этого утверждения интересующийся читатель может ознакомиться в видеоуроке.

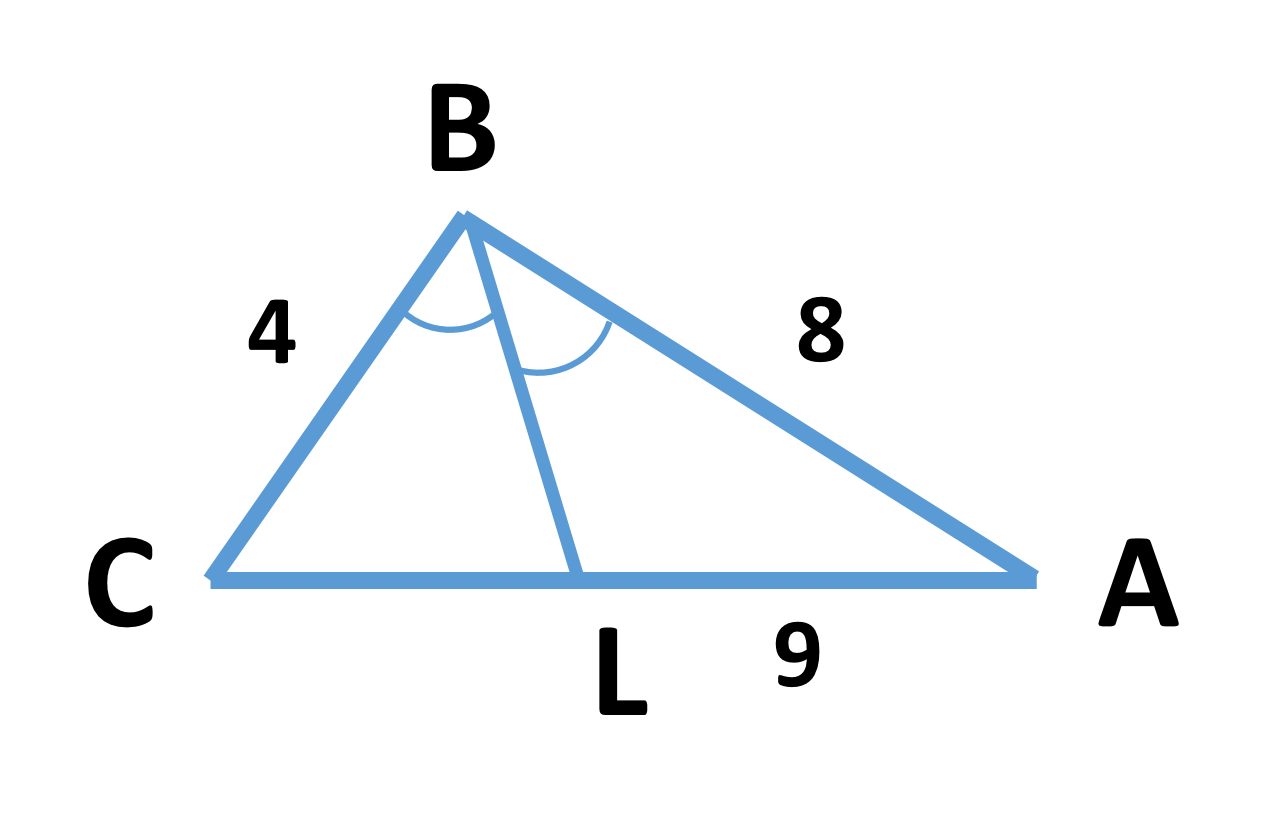
Пример 3. Дан треугольник со сторонами 4; 8; 9. Найти длину биссектрисы, проведенной к большей стороне.

Нахождение биссектрисы треугольника через длину сторон

Решение. Найдем сперва длины отрезков CL и LA. Используем для этого свойство биссектрисы треугольника. Биссектриса треугольника разбивает противоположную сторону на отрезки, пропорциональные прилежащим сторонам. То есть CL : CB = LA : BA или CL : 4 = LA : 8. Учитывая также, что CL + LA = 9, получаем, что CL = 3, LA = 6. По доказанной ранее теореме, длину биссектрисы BL можно найти по следующей формуле: BL2 = CB · BA — CL · LA = 4·8 — 3·6 = 14. Итак, BL = \sqrt{14}.

Задача для самостоятельного решения №3. В треугольнике ABC сторона AB равна 21, биссектриса BD равна 8\sqrt{7}, а отрезок DC равен 8. Найти периметр треугольника ABC.

Показать ответ
Ответ: 60.

Сергей Валерьевич
Репетитор по геометрии на Юго-Западной

Метки: , , , , , ,
Опубликовано в категории Методическая копилка | Нет комментариев »

Добавить комментарий