Если вы хотите, чтобы ваш ребёнок обучался в лицее «Вторая школа», вам стоит обратиться к репетитору, специализирующемуся на подготовке к вступительным экзаменам в это учебное заведение. Лицей №2 является одним из сильнейших образовательных учреждений г. Москвы физико-математической направленности. Количество абитуриентов растет с каждым годом, и поступить туда удаётся далеко не каждому. Поэтому помощь репетитора для поступления в лицей «Вторая школа» может оказаться очень кстати.
Репетитор о поступлении и учёбе в лицее «Вторая школа»
Чтобы стать его учеником лицея «Вторая школа», необходимо сдать вступительные экзамены по математике, которые состоят из двух блоков: письменного и устного. Цель письменной работы – выявление степени общей математической подготовки абитуриента, наличия необходимых навыков и знаний. На устном экзамене ученики решают логические задачи и выполняют задания на смекалку. Здесь они должны проявить свои способности к размышлению, рассуждению, умение делать верные умозаключения при помощи логики и находить оптимальное и наиболее рациональное решение без шаблонного алгоритма. Также проверяется пространственное мышление.
Обучение в лицее бесплатное, поэтому поступают туда только сильнейшие ученики. Учителя – кандидаты и доктора наук, которые дают детям прекрасное образование в области физики и математики.
Присутствуют элементы вузовской системы образования:
• семинары;
• лекции;
• зачеты и экзамены;
• практические работы.
Зачем нужен репетитор для подготовки к поступлению в лицей «Вторая школа»?
Есть вариант готовиться к поступлению в лицей «Вторая школа» самостоятельно, но, к сожалению, на это может просто не хватить времени. Только репетитор для поступления в лицей «Вторая школа» сможет составить индивидуальный план занятий и придерживаться его в процессе обучения, чтобы ваш ребёнок оказался готов к вступительным экзаменам вовремя.
На своих занятиях репетитор научит вашего ребёнка решать как стандартные задания, так и задания, требующие от ученика проявить смекалку и логику мышления (олимпиадные и нестандартные). Причём содержание последнего типа задач во многом отличается от математики, которой учат на уроках в школе. Зачастую они являются совершенно непривычными и незнакомыми для обычного рядового ученика. Поэтому репетитор для подготовки к поступлению в лицей «Вторая школа» должен иметь подготовленный банк таких заданий и четко отрегулированную обучающую систему.
За обучение ребенка решению олимпиадных задач берутся не многие репетиторы: это хлопотное и кропотливое дело, требующее тщательной подготовки к каждому занятию. Профессиональный репетитор способен обучить абитуриента решению этих задач, причём как по математике, так и по физике, чтобы успешно сдать вступительные экзамены. Он в состоянии дать ребенку все необходимое для поступления, проработать с ним нужные темы и задачи и подвести ученика к заветному поступлению.
На страницах этого сайта вы сможете найти всю необходимую информацию о профессиональном репетиторе по математике и физике, осуществляющем подготовку к вступительным экзаменам в лицей «Вторая школа». Вы также может самостоятельно оценить сложность предлагаемых на вступительном экзамене заданий. Ниже следует разбор примеров заданий, которые опубликованы на официальном сайте лицея. Попробуйте решить их самостоятельно, а затем сравните решение с приведённым в статье.
Разбор заданий вступительного экзамена в лицей «Вторая школа»
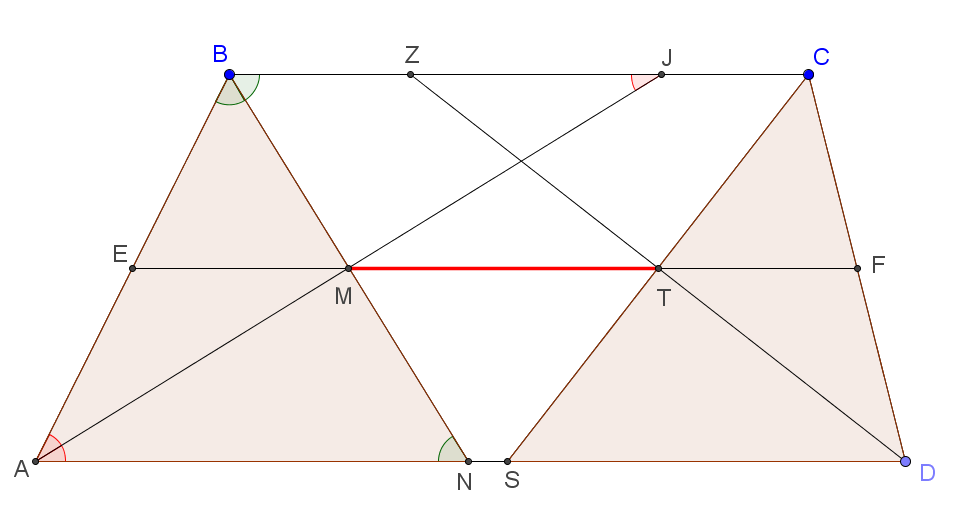
| 1. Сумма боковых сторон AB и CD трапеции ABCD равна b, а сумма её оснований равна a (a > b). Биссектрисы углов A и B пересекаются в точке M, а биссектрисы углов C и D пересекаются в точке T. Найдите MT. |
Проведём среднюю линию трапеции EF. Точками пересечения средней линии с биссектрисами BN и CS будут точки M и T, соответственно. Действительно, по теореме Фалеса BM = MN. Треугольник ABN — равнобедренный (∠CBN = ∠BNA, как накрест лежащие при параллельных прямых и секущей, ∠ABN = ∠CBN, так как BN — биссектриса, поэтому ∠ABN = ∠BNA). Следовательно, AM — биссектриса и медиана треугольника ABN.
Средняя линия трапеции равна полусумме оснований: ![]() . Тогда:
. Тогда:
![]()
Последнее получается из того, что EM и TF — средние линии треугольников ABN и SCD, соответственно). С учетом того, что треугольники ABN и CSD равнобедренные, получаем:
![]()
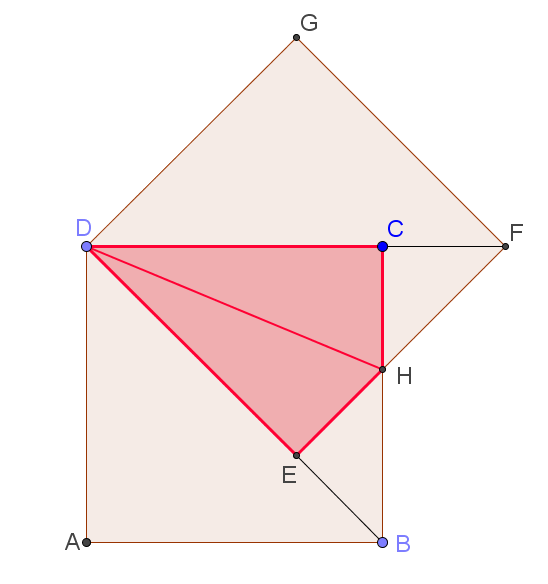
| 2. Квадрат с длиной стороны |
На рисунке прямоугольные треугольники EBH и HCF равны по катету (так как ![]() ) и острому углу (∠EHB = ∠CHF, так как они вертикальные). Тогда CH = HE и прямоугольные треугольники DCH и DHE равны по двум катетам.
) и острому углу (∠EHB = ∠CHF, так как они вертикальные). Тогда CH = HE и прямоугольные треугольники DCH и DHE равны по двум катетам.
Треугольник HCF — равнобедренный, при этом ![]() . Тогда искомая площадь равна
. Тогда искомая площадь равна ![]() кв. ед.
кв. ед.
| 3. Найдите 10 различных натуральных чисел, сумма которых делится на каждое из них. |
Сначала придумаем 3 различных натуральных числа, сумма которых делится на каждое из этих натуральных чисел. Очевидно, это числа 1, 2 и 3. Как получить четвёртое? Эта будет сумма первых трёх чисел. Действительно, ведь она будет отлична от них, но при этом с сумме с предыдущими числами будет делиться на саму себя (в результате будет получаться 2). И так далее.
Тогда искомый ряд: 1, 2, 3, 6, 12, 24, 48, 96, 192, 384.
| 4. Дано |
![]()
![]()
![]()
![]()
| 5. За два года население городка увеличилось на 44%. На сколько процентов увеличивалось население ежегодно (предполагается, что каждый год процент прироста населения одинаков)? |
Пусть за год прирост населения составлял ![]() %. Тогда за 2 года население вырастет в
%. Тогда за 2 года население вырастет в ![]() раз. Тогда имеет место равенство:
раз. Тогда имеет место равенство:
![]()
![]()
| 6. Составить квадратное уравнение, корни которого обратны корням уравнения |
Пусть корни квадратного уравнения ![]() равны
равны ![]() и
и ![]() . Тогда по теореме Виета
. Тогда по теореме Виета ![]() , а
, а ![]() .
.
Тогда для обратных корней имеем:
![]()
![]()
Тогда искомое квадратное уравнение, в соответствии с теоремой Виета, имеет вид:
![]()
| 7. Докажите, что при всех натуральных |
![]()
![]()
![]()
![]()
![]()
![]()
То есть при всех натуральных ![]() данное число может быть представлено в виде произведения двух чисел, каждое из которых отлично от 1.
данное число может быть представлено в виде произведения двух чисел, каждое из которых отлично от 1.
Вот такие задачи могут встретиться вам на вступительном экзамене по математике в лицей «Вторая школа». Если их решение не составило для вас труда, то вы вполне готовы к поступлению. Если же нет, самое время обратиться к профессиональному репетитору для подготовки в лицей «Вторая школа» со стажем. Удачи вам!

Необходим репетитор по физике и математике для поступления в 9 класс
Здравствуйте, Людмила. Я готовлю школьников к поступлению в лицей «Вторая школа». Подробную информацию о моих занятиях Вы можете найти на этой странице.
Здравствуйте, нам нужен репетитор для подготовки к вступительным экзаменам в 6 класс.
Здравствуйте, мои контакты можно найти на этой странице